Mekanika fluida
Mekanika fluida adalah subdisiplin dari mekanika kontinum yang mempelajari fluida (yang dapat berupa cairan dan gas). Mekanika fluida dapat dibagi menjadi fluida statik dan fluida dinamik. Fluida statis mempelajari fluida pada keadaan diam sementara fluida dinamis mempelajari fluida yang bergerak.
Hubungan dengan mekanika kontinum
Mekanika fluida biasanya dianggap subdisiplin dari mekanika kontinum, seperti yang diilustrasikan pada tabel berikut.
| Mekanika kontinum: studi fisika dari material kontinu | Mekanika solid: studi fisika dari material kontinu dengan bentuk tertentu. | Elastisitas: menjelaskan material yang kembali ke bentuk awal setelah diberi tegangan. | |
| Plastisitas: menjelaskan material yang secara permanen terdeformasi setelah diberi tegangan dengan besar tertentu. | Reologi: studi material yang memiliki karakteristik solid dan fluida. | ||
| Mekanika fluida: studi fisika dari material kontinu yang bentuknya mengikuti bentuk wadahnya. | Fluida non-Newtonian | ||
| Fluida Newtonian | |||
Dalam pandangan secara mekanis, sebuah fluida adalah suatu substansi yang tidak mampu menahan tekanan tangensial. Hal ini menyebabkan fluida pada keadaan diamnya berbentuk mengikuti bentuk wadahnya.
Asumsi Dasar
Seperti halnya model matematika pada umumnya, mekanika fluida membuat beberapa asumsi dasar berkaitan dengan studi yang dilakukan. Asumsi-asumsi ini kemudian diterjemahkan ke dalam persamaan-persamaan matematis yang harus dipenuhi bila asumsi-asumsi yang telah dibuat berlaku.
Mekanika fluida mengasumsikan bahwa semua fluida mengikuti:
- Hukum kekekalan massa
- Hukum kekekalan momentum
- Hipotesis kontinum, yang dijelaskan di bagian selanjutnya.
Kadang, akan lebih bermanfaat (dan realistis) bila diasumsikan suatu fluida bersifat inkompresibel. Maksudnya adalah densitas dari fluida tidak berubah ketika diberi tekanan. Cairan terkadang dapat dimodelkan sebagai fluida inkompresibel sementara semua gas tidak bisa.
Selain itu, terkadang viskositas dari suatu fluida dapat diasumsikan bernilai nol (fluida tidak viskos). Terkadang gas juga dapat diasumsikan bersifat tidak viskos. Jika suatu fluida bersifat viskos dan alirannya ditampung dalam suatu cara (seperti dalam pipa), maka aliran pada batas sistemnya mempunyai kecepatan nol. Untuk fluida yang viskos, jika batas sistemnya tidak berpori, maka gaya geser antara fluida dengan batas sistem akan memberikan resultan kecepatan nol pada batas fluida.
Hipotesis kontinum
Fluida disusun oleh molekul-molekul yang bertabrakan satu sama lain. Namun demikian, asumsi kontinum menganggap fluida bersifat kontinu. Dengan kata lain, properti seperti densitas, tekanan, temperatur, dan kecepatan dianggap terdefinisi pada titik-titik yang sangat kecil yang mendefinisikan REV (‘’Reference Element of Volume’’) pada orde geometris jarak antara molekul-molekul yang berlawanan di fluida. Properti tiap titik diasumsikan berbeda dan dirata-ratakan dalam REV. Dengan cara ini, kenyataan bahwa fluida terdiri dari molekul diskrit diabaikan.
Hipotesis kontinum pada dasarnya hanyalah pendekatan. Sebagai akibatnya, asumsi hipotesis kontinum dapat memberikan hasil dengan tingkat akurasi yang tidak diinginkan. Namun demikian, bila kondisi benar, hipotesis kontinum menghasilkan hasil yang sangat akurat.
Masalah akurasi ini biasa dipecahkan menggunakan mekanika statistik. Untuk menentukan perlu menggunakan dinamika fluida konvensial atau mekanika statistik, angka Knudsen permasalahan harus dievaluasi. Angka Knudsen didefinisikan sebagai rasio dari rata-rata panjang jalur bebas molekular terhadap suatu skala panjang fisik representatif tertentu. Skala panjang ini dapat berupa radius suatu benda dalam suatu fluida. Secara sederhana, angka Knudsen adalah berapa kali panjang diameter suatu partikel akan bergerak sebelum menabrak partikel lain.
Persamaan Navier-Stokes (dinamakan dari Claude-Louis Navier dan George Gabriel Stokes) adalah serangkaian persamaan yang menjelaskan pergerakan dari suatu fluida seperti cairan dan gas. Persamaan-persamaan ini menyatakan bahwa perubahan dalam momentum (percepatan) partikel-partikel fluida bergantung hanya kepada gaya viskos internal (mirip dengan gaya friksi) dan gaya viskos tekanan eksternal yang bekerja pada fluida. Oleh karena itu, persamaan Navier-Stokes menjelaskan kesetimbangan gaya-gaya yang bekerja pada fluida.
Persamaan Navier-Stokes memiliki bentuk persamaan diferensial yang menerangkan pergerakan dari suatu fluida. Persaman seperti ini menggambarkan hubungan laju perubahan suatu variabel terhadap variabel lain. Sebagai contoh, persamaan Navier-Stokes untuk suatu fluida ideal dengan viskositas bernilai nol akan menghasilkan hubungan yang proposional antara percepatan (laju perubahan kecepatan) dan derivatif tekanan internal.
Untuk mendapatkan hasil dari suatu permasalahan fisika menggunakan persamaan Navier-Stokes, perlu digunakan ilmu kalkulus. Secara praktis, hanya kasus-kasus aliran sederhana yang dapat dipecahkan dengan cara ini. Kasus-kasus ini biasanya melibatkan aliran non-turbulen dan tunak (aliran yang tidak berubah terhadap waktu) yang memiliki nilai bilangan Reynold kecil.
Untuk kasus-kasus yang kompleks, seperti sistem udara global seperti El Niño atau daya angkat udara pada sayap, penyelesaian persamaan Navier-Stokes hingga saat ini hanya mampu diperoleh dengan bantuan komputer. Kasus-kasus mekanika fluida yang membutuhkan penyelesaian berbantuan komputer dipelajari dalam bidang ilmu tersendiri yaitu mekanika fluida komputasional
Bentuk umum persamaan
Bentuk umum persamaan Navier-Stokes untuk kekekalan momentum adalah :
di mana
- ρ adalah densitas fluida,
 adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)
adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)
 adalah vektor kecepatan,
adalah vektor kecepatan,- f adalah vektor gaya benda, dan
 adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.
adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.
 adalah tensor yang simetris kecuali bila fluida tersusun dari derajat kebebasan yang berputar seperti vorteks. Secara umum, (dalam tiga dimensi)
adalah tensor yang simetris kecuali bila fluida tersusun dari derajat kebebasan yang berputar seperti vorteks. Secara umum, (dalam tiga dimensi)  memiliki bentuk persamaan:
memiliki bentuk persamaan:
di mana
- σ adalah tegangan normal, dan
- τ adalah tegangan tangensial (tegangan geser).
Persamaan di atas sebenarnya merupakan sekumpulan tiga persamaan, satu persamaan untuk tiap dimensi. Dengan persamaan ini saja, masih belum memadai untuk menghasilkan hasil penyelesaian masalah. Persamaan yang dapat diselesaikan diperoleh dengan menambahkan persamaan kekekalan massa dan batas-batas kondisi ke dalam persamaan di atas.
Fluida Newtonian vs. non-Newtonian
Sebuah Fluida Newtonian (dinamakan dari Isaac Newton) didefinisikan sebagai fluida yang tegangan gesernya berbanding lurus secara linier dengan gradien kecepatan pada arah tegak lurus dengan bidang geser. Definisi ini memiliki arti bahwa fluida newtonian akan mengalir terus tanpa dipengaruhi gaya-gaya yang bekerja pada fluida. Sebagai contoh, air adalah fluida Newtonian karena air memiliki properti fluida sekalipun pada keadaan diaduk.
Sebaliknya, bila fluida non-Newtonian diaduk, akan tersisa suatu "lubang". Lubang ini akan terisi seiring dengan berjalannya waktu. Sifat seperti ini dapat teramati pada material-material seperti puding. Peristiwa lain yang terjadi saat fluida non-Newtonian diaduk adalah penurunan viskositas yang menyebabkan fluida tampak "lebih tipis" (dapat dilihat pada cat). Ada banyak tipe fluida non-Newtonian yang kesemuanya memiliki properti tertentu yang berubah pada keadaan tertentu.
Persamaan pada fluida Newtonian
Konstanta yang menghubungkan tegangan geser dan gradien kecepatan secara linier dikenal dengan istilah viskositas. Persamaan yang menggambarkan perlakuan fluida Newtonian adalah:
di mana
- τ adalah tegangan geser yang dihasilkan oleh fluida
- μ adalah viskositas fluida-sebuah konstanta proporsionalitas
 adalah gradien kecepatan yang tegak lurus dengan arah geseran
adalah gradien kecepatan yang tegak lurus dengan arah geseran
Viskositas pada fluida Newtonian secara definisi hanya bergantung pada temperatur dan tekanan dan tidak bergantung pada gaya-gaya yang bekerja pada fluida. Jika fluida bersifat inkompresibel dan viskositas bernilai tetap di seluruh bagian fluida, persamaan yang menggambarkan tegangan geser (dalam koordinat kartesian) adalah
di mana
- τij adalah tegangan geser pada bidang ith dengan arah jth
- vi adalah kecepatan pada arah ith
- xj adalah koordinat berarah jth
Jika suatu fluida tidak memenuhi hubungan ini, fluida ini disebut fluida non-Newtonian.

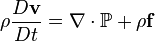













 Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.
Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.





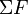 adalah resultan
adalah resultan 
 adalah
adalah